1=2 A Proof using Beginning Algebra The Fallacious Proof Step 1 Let a=b Step 2 Then , Step 3 , Step 4 , Step 5 , Step 6 and Step 7 This can be written as , Step 8 and cancelling the from both sides gives 1=2 See if you can figure out in which step the fallacy liesArchimedes ( BC) also derived the formula 1^2 2^2 3^2 n^2 = n(n 1)(2n 1)/6 for the sum of squares Fill in any missing details in the following sketch of his proofAnd the righthand side of (*) is (1)(2)(3)/3 = 2 So (*) holds for n = 1 Assume, for n = k, that (*) holds;

P N 1 3 3 2 3 N 1 3 N 1 2 If P K Is True Prove P K 1 Is True 5mzjtebb Mathematics Topperlearning Com
1^2+3^2+5^2+...+n^2 formula
1^2+3^2+5^2+...+n^2 formula-< n^n Prove that 3^n < n!6 P ALEXANDERSSON Solution6 (a) Base case is n= 2The left hand side is just 1−1 4 while the right hand side is 3 4, so both sides are equal Suppose now that Yn j=2 1− 1 j2 n1 2n for some n≥2 After multiplying both sides with 1− 1 (n1)2 we getnY1 j=2 1−



Python Challenges 1 Exercises Practice Solution W3resource
#= 1^2 2^2 3^2 The #N# th term would be given by #(1)^(N1)N^2# , and the finite sum at the #N# th term would be found as follows If this series were not alternating, the sum would have beenShow that 1^3 2^3 n^3 = (1 2 3 n)^2 for n greaterthanorequalto1 Prove by induction for n > 1 n!The sum of the first n squares, 1 2 2 2 n 2 = n(n1)(2n1)/6 For example, 1 2 2 2 10 2 =10×11×21/6=385 This result is usually proved by a method known as mathematical induction, and whereas it is a useful method for showing that a formula is true, it does not offer any insight into where the formula comes from
2/3 1/2 = 1/6 in fraction form 2/3 1/2 = in decimal form This calculator, formula, step by step calculation and associated information to find the difference between 2/3 & 1/2 may help students, teachers, parents or professionals to learn, teach, practice or verify such two fractions subtraction calculations efficiently2/3 1/2 The calculator performs basic and advanced operations with fractions, expressions with fractions combined with integers, decimals, and mixed numbers It also shows detailed stepbystep information about the fraction calculation procedure Solve problems with two, three, or more fractions and numbers in one expressionWhich is true Inductive Step Fix k 1, and suppose that Pk holds, that is, 1 22 3 (2k)2 = k(2k 1)(4k 1) 3 It
Anonymous said Help me Write a C or Java program to find out the sum of series 1! Question Find the sum of the series 1 2 2 2 3 2 4 2 5 2 n terms My attempt I took two terms of the series as (2k1) 2 (2k) 2 = 14k So adding the series as ∑ (14k) taking range of k from 1 to n/2 (since I'm taking two terms at the same time), I got the answer n(n1)/2 but my textbook has given the answer as n(2n4 Find and prove by induction a formula for Q n i=2 (1 1 2), where n 2Z and n 2 Proof We will prove by induction that, for all integers n 2, (1) Yn i=2 1 1 i2 = n 1 2n Base case When n = 2, the left side of (1) is 1 1=22 = 3=4, and the right side is (21)=4 = 3=4, so both sides are equal and (1) is true for n = 2 2




Answered Use Mathematical Induction To Prove The Bartleby




n2 Formula Proof
The partial sums of the series 1 2 3 4 5 6 ⋯ are 1, 3, 6, 10, 15, etcThe nth partial sum is given by a simple formula = = () This equation was knownIn example to get formula for $1^22^23^2n^2$ they express $f(n)$ as $$f(n)=an^3bn^2cnd$$ also known that $f(0)=0$, $f(1)=1$, $f(2)=5$ and $f(3)=14$ Then this values are inserted into function, we get system of equations solve them and get a,b,c,d coefficients and we get that $$f(n)=\frac{n}{6}(2n1)(n1)$$Solve for n 2/3*(1n)=1/2n Simplify Tap for more steps Apply the distributive property Multiply by Combine and Combine and Move all terms containing to the left side of the equation Tap for more steps Add to both sides of the equation To write as a
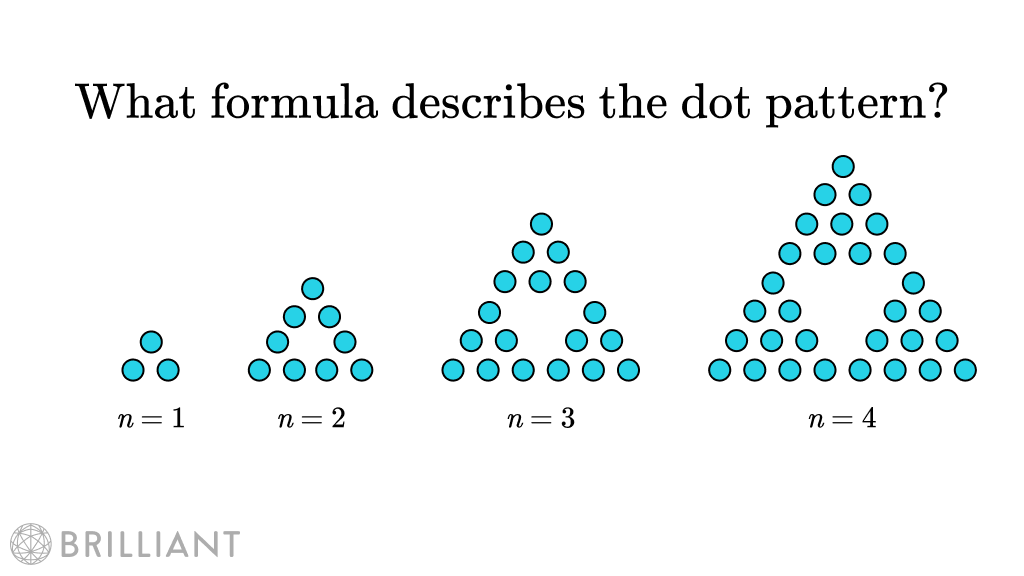



Brilliant Org Which Formula Describes The Number Of Dots In This Pattern A 3 2n 1 B 3n N 1 2 C 3 N D 3 6 N 1




5 4 Mathematical Induction T
That is, assume that 1×2 2×3 3×4 (k)(k1) = (k)(k1)(k2)/3 Let n = k 1 The lefthand side of (*) then gives usProblems on Binomial Theorem Question 1 If the third term in the binomial expansion of equals 2560, find x Solution ⇒ (log 2x) 2 = 4 ⇒ log 2x = 2 or 2 ⇒ x = 4 or 1/4 Question 2 Find the positive value of λ for which the coefficient of x2 in the expression x2√ x32 Solving n23n2 = 0 by Completing The Square Subtract 2 from both side of the equation n23n = 2 Now the clever bit Take the coefficient of n , which is 3 , divide by two, giving 3/2 , and finally square it giving 9/4 Add 9/4 to both sides of the equation On the right hand side we have




Factorial Calculator Solve N Inch Calculator



Http Www Math Drexel Edu Dmitryk Teaching Math221 Spring 12 Quiz4 Solutions Pdf
What is the value of 1 × 1!Formula for the sum 1 2 2 2 3 2 ⋯ n 2 1^2 2^2 3^2 \cdots n^2 1 2 2 2 3 2 ⋯ n 2 Suppose we have the following sum S n = 1 2 2 2 3 2 ⋯ n 2 = ∑ i = 1 n i 2The formula 1 22 32 (2n)2 = n(2n1)(4n1) 3 Solution For any integer n 1, let Pn be the statement that 1 22 3 (2n)2 = n(2n1)(4n1) 3 Base Case The statement P1 says that 1 22 = (1)(2(1)1)(4(1)1) 3 = 3(5) 3 = 5;



Solved The Explicit Formula For A Sequence Is An 2 3 2 N 1 What Is The 21st Term Of The Sequence 2 The Explicit Formula For A Sequence Is Course Hero



1
Find 2,2,4trimethyl3 dihydro1H1,5 benzodiazepine and related products for scientific research at MilliporeSigmaCompute answers using Wolfram's breakthrough technology & knowledgebase, relied on by millions of students & professionals For math, science, nutrition, historyView solution If a n 1 = a n − n 2 n and a 1 = 3 then the value of ∣ a 2 0 − a 1 5 ∣ =




Problem 2 1 Show That For Any Positive Integer N We Chegg Com




1234n Formula
S_n = 1234\cdots n = \displaystyle \sum_ {k=1}^n k S n = 12 34⋯ n = k=1∑n k The elementary trick for solving this equation (which Gauss is supposed to have used as a child) is a rearrangement of the sum as follows S n = 1 2 3 ⋯ n S n = n n − 1 n − 2 ⋯ 1 suppose s 1 2 3 n term also s n n 1 n 2 3 2 1 adding that 2s n 1 n 1 n 1 n 1 n 1 n 1 n 1 2s Answer added by Md Mozaffor Hussain Mozaffor, Assistant Teacher , BIAM$\begingroup$ Note, if you wanted to subvert the problem stated, you could perform induction separately on $\sum n^2$ and $\sum n$ $\endgroup$ – halfinteger fan Feb 2 '13 at 13
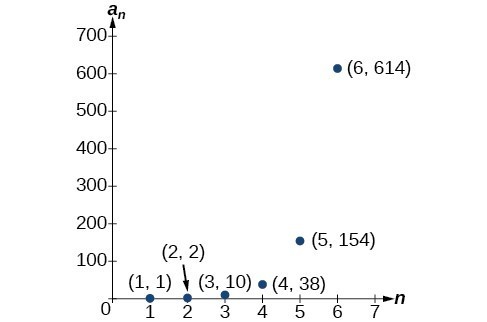



Writing The Terms Of A Sequence Defined By A Recursive Formula College Algebra




Math 6 Section 700 Experimentation Conjecture And Reasoning Spring 05
(n 1) = (𝑛(𝑛 1)(𝑛 2))/3 Let P(n) 12 23 34 n(n 1) = (𝑛(𝑛 1)(𝑛 2))/3 For n = 1, LHS = 12 = 2 RHS = (1(11)(12))/3 = 123/3 = 2 LH (टीचू)If n is greater than 6For example 1/2 and 2/4 are equivalent, y/(y1) 2 and (y 2 y)/(y1) 3 are equivalent as well To calculate equivalent fraction, multiply the Numerator of each fraction, by its respective Multiplier




Art Of Problem Solving




Show That N N 1 2n 1 Is Multiple Of 6 For Every Natural Number N
Find the sum ∑ r = 1 n r (r 1) 1 2 2 2 3 2 r 2 ?To do this, we will fit two copies of a triangle of dots together, one red and an upsidedown copy in green Eg T (4)=1234Let S be the sum of squares of the first n natural numbers, such that S=1^22^2n^2 Our aim is to derive a closed form formula for S in terms of n We have (x1)^3= (x1) (x^22x1) implies (x1)^3=x^33x^23x1 Using this, we write the following sequence of equations where 1≤x≤n




Solved Use Iteration Guess Explicit Formula Please Solve Problem 2 Please Solve Using Arithmetic Q



Python Challenges 1 Exercises Practice Solution W3resource
The principle of mathematical induction is used to prove that a given proposition (formula, equality, inequality) is true for all positive integer numbers greater than or equal to some integer N Prove that 1 2 2 2 3 2 n 2 = n (n 1) (2n 1)/ 6 For all positive integers nGraph y=2(x1)^22 Find the properties of the given parabola Tap for more steps Use the vertex form, Substitute the known values of , , and into the formula and simplify Find the axis of symmetry by finding the line that passes through the vertex and the focus Find the directrix Given an integer N, the task is to find the sum of series 2 0 2 1 2 2 2 3 2 n Examples Input 5 Output 31 2 0 2 1 2 2 2 3 2 4 = 1 2 4 8




Pdf Important Sum Formulas Omid Motahed Academia Edu




1 2 2 3 3 4 N N 1 Formula Novocom Top
Simple and best practice solution for 3/2t=1/2 equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, Another approach Using formula to find sum of series 1 2 3 2 5 2 7 2 (2*n 1) 2 = (n * (2 * n 1) * (2 * n 1)) / 3 Please refer sum of with n = 5, the series 1^2 2^2 3^2 n^2 = = 55 Sum n^2 = ( n / 6 )( n 1 )( 2n 2 ) = (5 / 6) * 6 * (2*5 2) = 5 * 12 = 60!




Is This Modern Programming Interview Challenge S Solution Unreliable Stack Overflow




Ramanujan S Sum Wikipedia
N, with N input from keyboard 5/27/13, 551 AMIn mathematics, the infinite series 1 / 2 1 / 4 1 / 8 1 / 16 ··is an elementary example of a geometric series that converges absolutelyThe sum of the series is 1 In summation notation, this may be expressed as = = = The series is related to philosophical questions considered in antiquity, particularly to Zeno's paradoxes 21 For the proof, we will count the number of dots in T (n) but, instead of summing the numbers 1, 2, 3, etc up to n we will find the total using only one multiplication and one division!




In Exercises 5 18 Use Mathematical Induction To Chegg Com



2
In Exercises 115 use mathematical induction to establish the formula for n 1 1 12 22 32 n2 = n(n 1)(2n 1) 6 Proof For n = 1, the statement reduces to the given statement is true for every positive integer n 2 3 32 33 3n = 3n1 3 2 Proof For n = 1, the statement reduces to 3 = 32 3 2 and is obviously true Assuming2/3 (1n)=1/2n Simple and best practice solution for 2/3 (1n)=1/2n equation Check how easy it is, and learn it for the future Our solution is simple, and easy to understand, so don`t hesitate to use it as a solution of your homework If it's not what You are looking for type in the equation solver your own equation and let us solve it3/2 = 2 1/2 7/4 = 2 1/4 15/8 = 2 1/8 and so on;



How To Calculate 1 2 3 4 5 6 7 8 9 10 Quickly Quora




Different Formulas On Permutation Tutorsonnet
Prove by Induction 1^2 2^2 3^2 4^2 n^2 = (n(n1)(2n1))/6 Example 1 For all n ≥ 1, prove that 12 22 32 42 n2 = (n(n1)(2n1))/6Let P (n) 12 22 32 42 n2 = (n(n1)(2n1))/6For n = 1, LHS = 12 = 1 RHS = (1(11)(2 × 1 1))/6 = (1 × 2 × 3)/6 = 1Hence, LHS = RHS ∴ P(n) is true for n = 1Assume thatEnter expression with fractions1/3 2/4 1/2 The calculator performs basic and advanced operations with fractions, expressions with fractions combined with integers, decimals, and mixed numbers It also shows detailed stepbystep information about the fraction calculation procedure Solve problems with two, three, or more fractions andHere is a pattern which does not depend on n Multiply by 3 3 3^2 3^n1 3^n = 3S Subtract the first from the second 1 00 0 3^n = 2S Divide by 2 and you have your solution Using induction is possible, but does not add to the understanding of most students At a key level, I believe in Street Fighting mathematics




Find The Sum To N Terms 1 2 3 2 5 2 Youtube




What Is The Formula For The General Term Math A N Math Of The Sequence Math 5 1 5 1 5 1 Math Quora
Means n factorial or n(n1) (n2) 1 a) n × (n 1) × (n 1)!The nth finite sum is 2 1/2^n This converges to 2 as n goes to infinity, so 2 is the value of the infinite sum Submit Your Own Question Create a Discussion Topic This part of the site maintained by (No Current Maintainers)`1222^232^3n2^n=(n1)2^(n1)2` Step by step solution by experts to help you in doubt clearance & scoring excellent marks in exams




The Wallis Product Formula For Pi And Its Proof Mind Your Decisions




The Catalan Numbers And Their Applications 1 2
Explanation using the method of proof by induction this involves the following steps ∙ prove true for some value, say n = 1 ∙ assume the result is true for n = k ∙ prove true for n = k 1 n = 1 → LH S = 12 = 1 and RHS = 1 6 (1 1)(2 1) = 1 ⇒result is true for n = 1 That means that the total number of compare/swaps you have to do is (n 1) (n 2) This is an arithmetic series, and the equation for the total number of times is (n 1)*n / 2 Example if the size of the list is N = 5, then you do 4 3 2 1 = 10 swaps and notice that 10 is the same as 4 * 5 / 2Find 1,2 Benzisothiazol 3(2H)one and related products for scientific research at MilliporeSigma




The Catalan Numbers And Their Applications Ppt Video Online Download
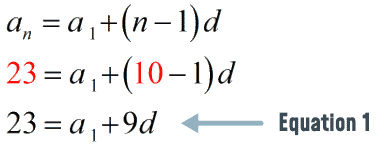



Arithmetic Series Formula Chilimath
Hi Zamira, I want to state the problem more precisely Prove that 122 2 2 3 2 n1 = 2 n 1 for n = 1, 2, 3, There are two steps in a proof by induction, first you need to show that the result is true for the smallest value on n, in this case n = 1




A Oeis




5 4 Mathematical Induction T



1




Proof Of Finite Arithmetic Series Formula By Induction Video Khan Academy




Solutions To Math Problems Sine Special Functions



4 1 Higher Order Derivatives



Http Www Math Pitt Edu Athanas Math 0230 Calculus Ii Practice8answers Pdf




Formula 1 2 3 4




Prove By Induction Sum Of The First N Cubes 1 3 2 3 3 3 N 3 Youtube




Solved Use Iteration Guess Explicit Formula Sequence Tk Tk 1 3k 1 Integers K 1 T0 0 Q



1




Answered I Proving A Formula Use Mathematical Bartleby



4 1 2 3 8 2 3 4 16 3 4 5 Nterms Prove That By Induction That 2 N 2 N 2 2 Brainly In




More On Sequences Some Sequences Are Not Arithmetic
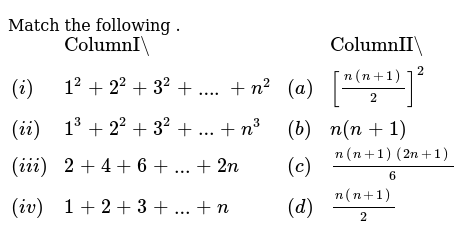



Mathod Of Induction 1 2 2 2 3 2 N 2 N N 1 2n 1 6




Find The Sum Of The First 2n Terms Of The Series 1 2 2 3 2 4 5 2 6 Brainly In




Rd Sharma Solutions For Class 11 Maths Updated 21 22 Chapter 19 Arithmetic Progressions Download Free Pdf




P N 1 3 3 2 3 N 1 3 N 1 2 If P K Is True Prove P K 1 Is True 5mzjtebb Mathematics Topperlearning Com
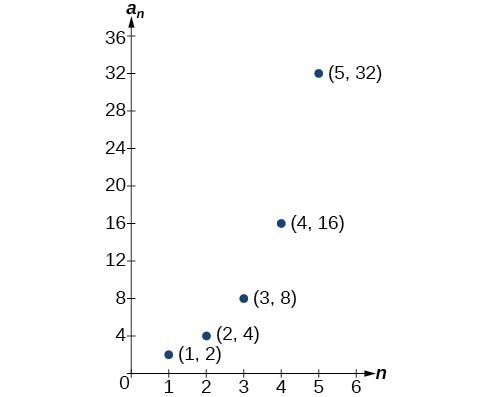



Sequences Defined By An Explicit Formula College Algebra




Is There Any Elementary Formula For The Sequence Sum K 1 N Left 2k 1 Right Left Frac 1 2 Right K Mathematics Stack Exchange




The Wallis Product Formula For Pi And Its Proof Mind Your Decisions




A Use Gauss S Approach To Find The Following Sum Math 2 4 6 Ldots 100 Math B Use Gauss S Approach To Find A Formula For The Sum Of




Math 1210 Solutions To Assignment 1 Fall 12 1 A Use
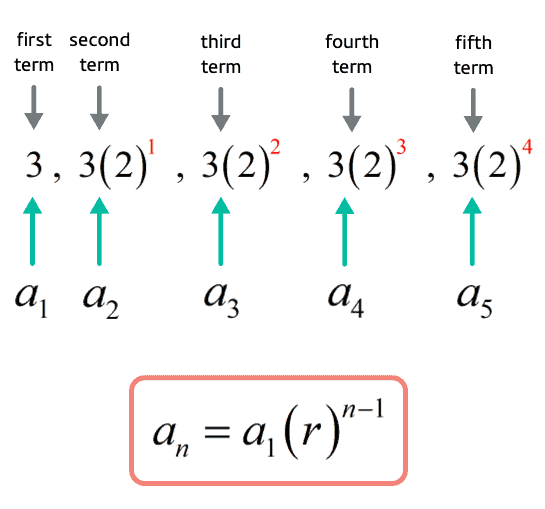



Geometric Sequence Formula Chilimath




Geometric Series Wikipedia




Answered And N 2n 1 N 1 3 5 13 The Bartleby
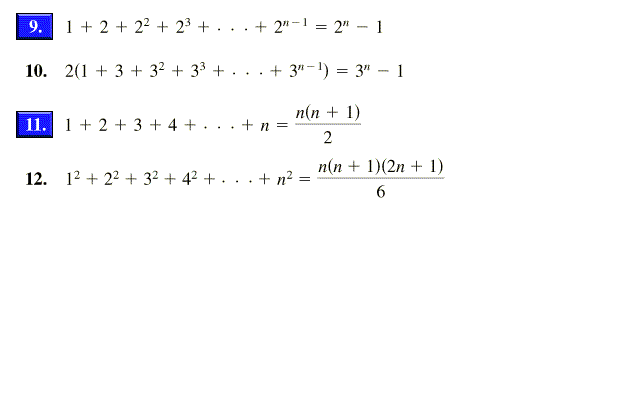



In Exercises 5 18 Use Mathematical Induction To Chegg Com




Sum To N Terms Of Special Series Study Material For Iit Jee Askiitians



Key Concepts In Computer Science Assignment 10 All Test Answers




James Tanton What S The Next Number In The Sequence 2 4 6 8 Write A Formula That Gives 2 For N 1 4 For N 2 6 For N 3 8 For




Chapter 1




Prove By Mathematical Induction 3 4 5 N 2 N N Homeworklib




Product N K 2 1 1 K 2 1 1 2 2 1 1 3 2 Chegg Com



Users Math Msu Edu Users Magyarp Math299 Ws8 Solutions Pdf




How To Create A Flow Chart For Sum Of Squares For N Integers Testingdocs Com
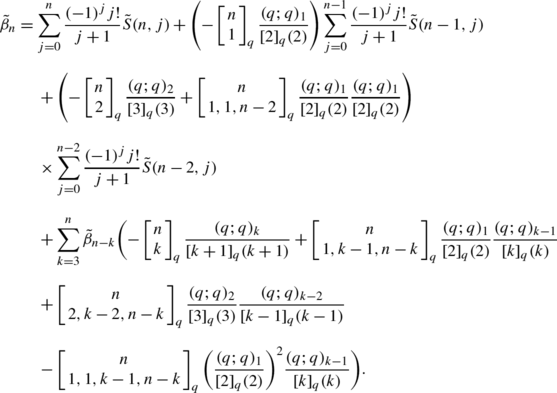



On A Q Analogue For Bernoulli Numbers Springerlink
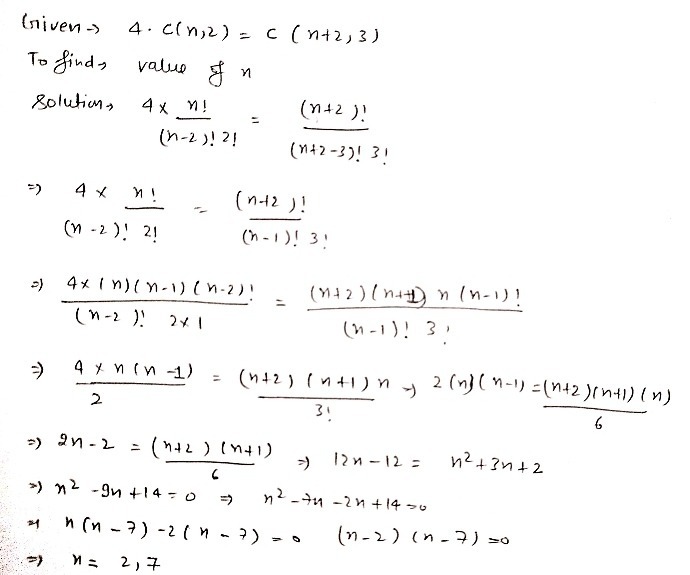



Example 7 Find N When 4 Cn 2 Cn 2 3 Solution Gauthmath




Prove That 1 2 2 2 3 2 N 2 N N 1 2n 1 6




Proof Of 1 2 2 2 Cdots N 2 N 3 3 N 2 2 N 6 Mathematics Stack Exchange




Fascinating Triangular Numbers By Shyam Sunder Gupta




Prove That 1 3 2 3 3 3 N 3 N N 1 2 2 Teachoo




Prove That 1 3 2 3 3 3 N 3 N N 1 2 2 Teachoo




Special Series Definition Theorem Example Solution Mathematics




Recursive Definitions Consider The Integer Sequence B B B Where Bn 2n For All N ℤ It Is Then Found That B 2 0 0 B 2 1 2 B 2 2 4 And So On If B Needed To Be




Geometric Series Wikipedia




Example 3 Let Sequence Be A1 1 An An 1 2 Examples



Users Math Msu Edu Users Lawrence Sept6hmwks Pdf




Complete The Following Use Arithmetic To Evaluate Chegg Com



Www Topperlearning Com Answer The Arithmetic Mean Of 1 2 3 N Is A N 1 2 B N 1 2 C N 2 D N 2 1 Bsxytqss




For Each Of The Following Functions Indicate How Much The Function S



Prove That 1 2 2 2 3 2 N 2 N N 1 2n 1 6 Youtube




Sum Of Squares Of Odd Numbers 1 2 3 2 5 2 2n 1 2 Derivation Formula Prmo Rmo Iit Youtube




Proof Uniquely Mathematical And Creative Ppt Download



Search Q 1 2b1 2 2b1 4 2b 2b1 N Formula Tbm Isch



2




Prove 1 2 3 N N N 1 2 Mathematical Induction



Http Dx Doi Org 10 2307




Math Mathtricks Physics Physics Formulas Math Methods Studying Math Logic Math




Using Sum Of Squares Triangle To Prove Sum Of Squares Formula Mtg My Triangle Geometry
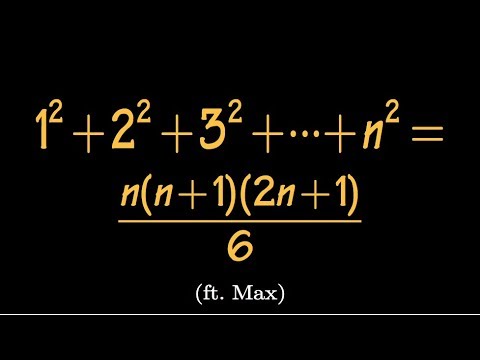



Find The Sum Of First N Squares Difference Equation Approach Ft Max Youtube




Solved 3 14 Proving A Formula Use Mathematical In
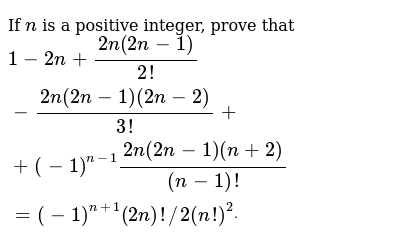



Finding A Formula For Fnfn F0 1 F1 2 Fn 2fn 2f0 1 F1 2 Fn 2fn 2



Finding The Sum Of Consecutive Numbers



Establish A Formula For 1 1 4 1 1 9 1 1 N 2 Stumbling Robot




Just Need Help Finding The A 3 N General Formula Chegg Com



Solved Q1 Which Of The Following Shows The Correct First Step To Prove The Following By Mathematical Induction Course Hero



Finding Proof For The Single Direction Paper Folding Theorem Mathhelp




n2 Formula




How To Derive N 1 2 From 1 2 3 N N Quora



In The Sequence Of Sets 1 2 3 4 5 6 7 8 9 10 And So On What Is The Sum Of Elements In The 50th Set Quora




Given The Sequence An Defined Recursively As Follows An 3an 1 2 For N 2 1 Al Terms Of A Sequence Homeworklib




2 Write A Formula For The Px13n Term For Each S Gauthmath
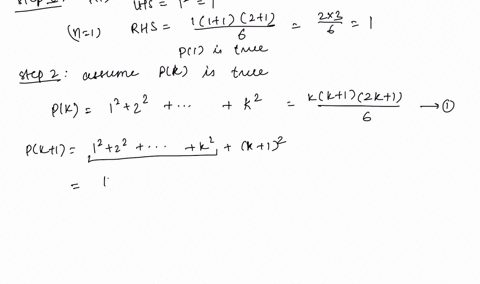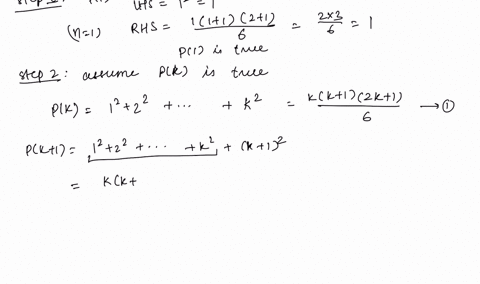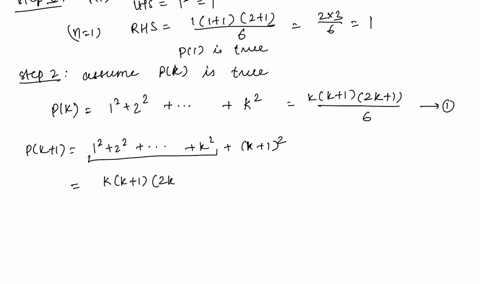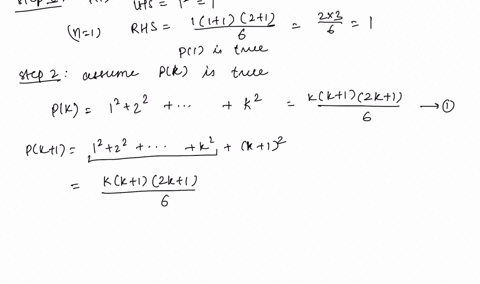



Solved Use Mathematical Induction To Prove That T
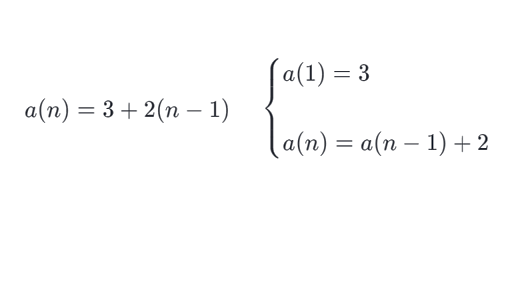



Intro To Arithmetic Sequence Formulas Algebra Article Khan Academy



0 件のコメント:
コメントを投稿